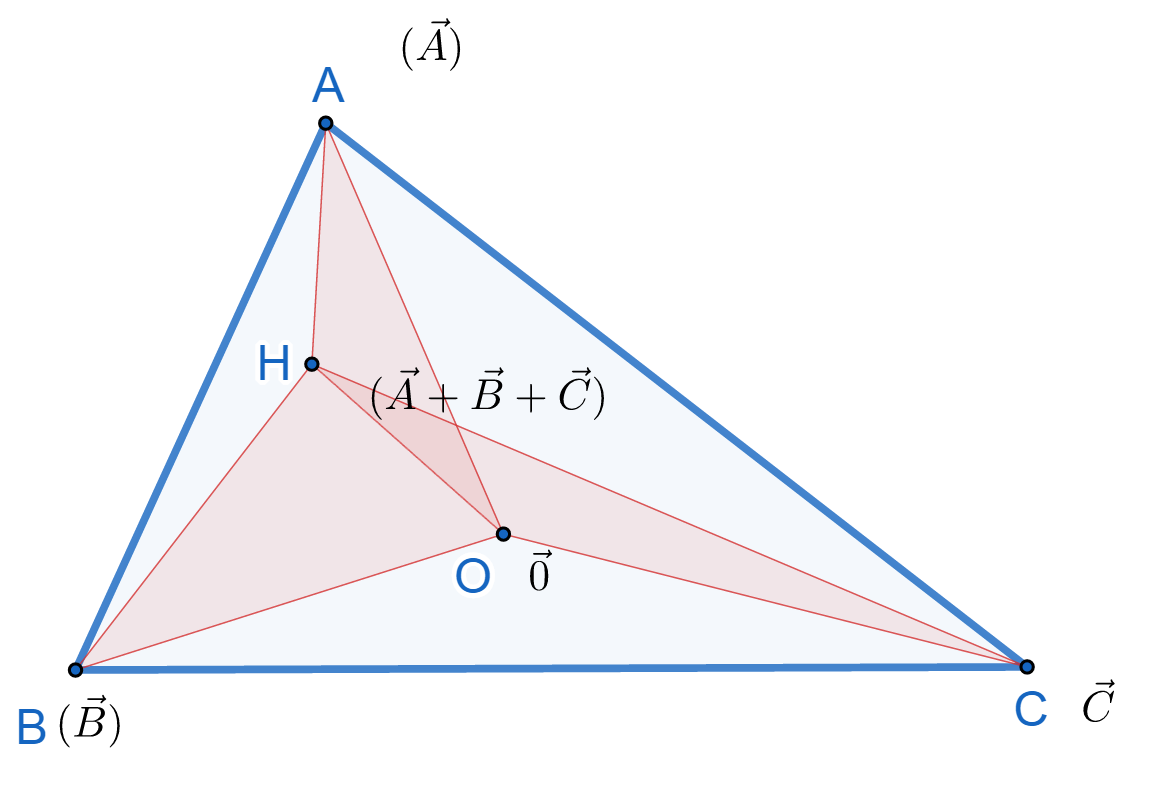
Following is a proof using vectors. Let's denote position vector of point P by $$\vec{P}$$

Let $$\vec{O}=\vec{0}$$,  and then observe that $$\vec{H}=\vec{A}+\vec{B}+\vec{C}$$

Now let signed area of a triangle ABC be (we consider its sign as positive if A,B,C are in antclockwise direction) denoted by (ABC)

Now observe that $$(ABC)=\frac{1}{2}\vec{BC}\times \vec{BA}=\frac{1}{2}(\vec{B}\times\vec{C}+\vec{C}\times\vec{A}+\vec{A}\times\vec{B})$$

Hence we have

• $$(AOH)=\frac{1}{2}(\vec{A}+\vec{B}+\vec{C})\times\vec{A}$$
• $$(BOH)=\frac{1}{2}(\vec{A}+\vec{B}+\vec{C})\times\vec{B}$$
• $$(COH)=\frac{1}{2}(\vec{A}+\vec{B}+\vec{C})\times\vec{C}$$

Now if not all three of them are 0, then there are two of the above three signed area have same sign. WLOG let's consider (BOH) and (COH) have same sign, then

$$|AOH|=|-(BOH)-(COH)|=|BOH+COH|=|BOH|+|COH|$$

Hence we have our desired result.