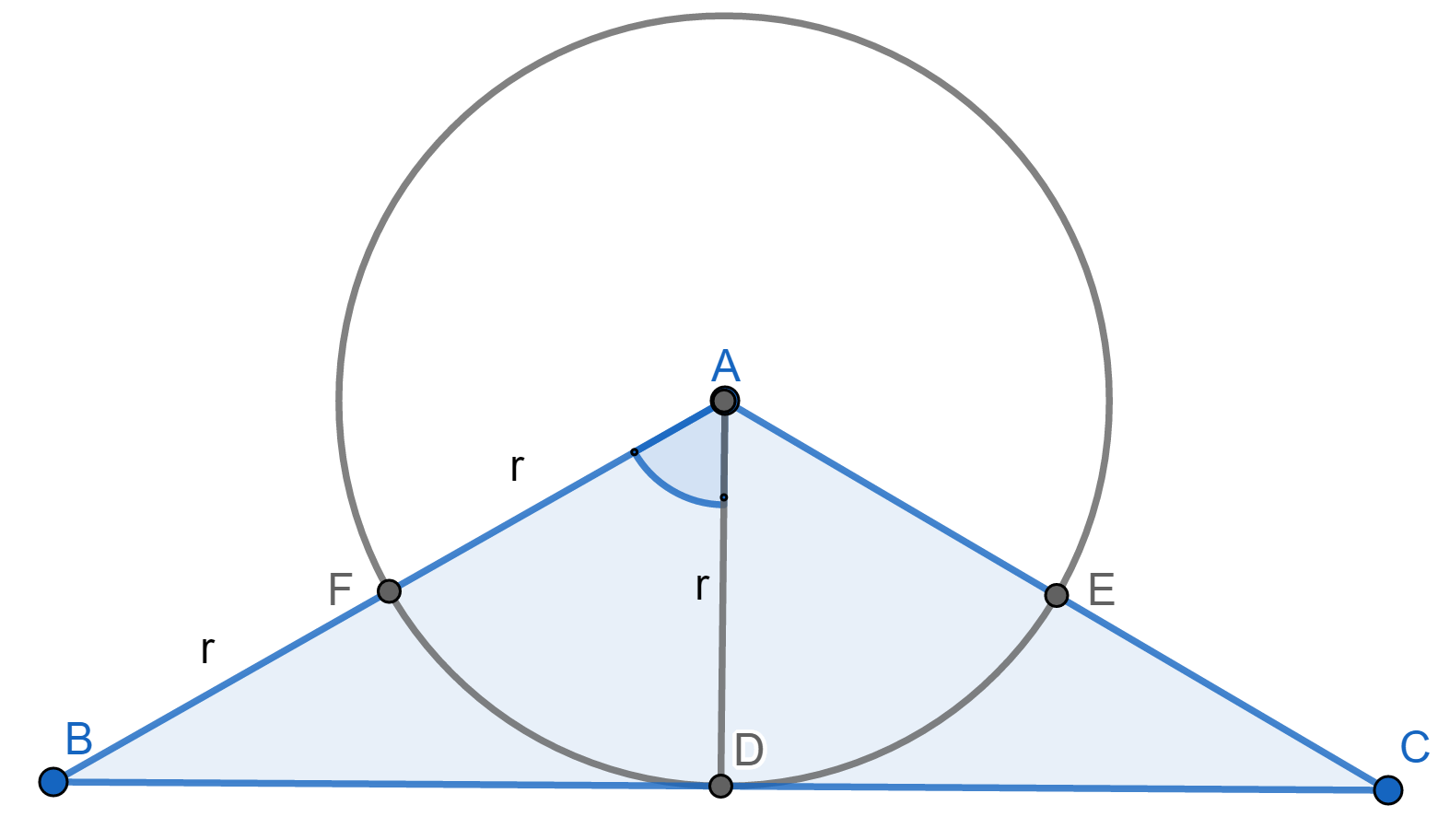
Let D, E, F be midpoints of sides BC, CA, AB respectively. Hence the circle in the above figure is the nine-point circle of triangle ABC

If vertex A is the nine-point center of triangle ABC then following are some of the observations

• AE=AF=r (radius of the circle in the above figure). Therefore AB=AC=2r, hence this condition was redundant.
• AD=r. Since triangle ABC is isosceles, therefore AD is also an altitude, i.e. $$\angle ADC=90^\circ$$
• $$\frac{AD}{AB}=\frac{1}{2}\Longrightarrow \angle BAD=60^\circ$$.

Also observe that whenever in a $$\triangle XYZ, \angle  YXZ=120^\circ \& XY=XZ$$, then X is a nine-point center of triangle XYZ

Hence A is a nine-point center of a triangle ABC if and only if-$$\angle BAC=120^\circ \& AB=AC$$