New Home › Forums › Math Olympiad - RMO and INMO › INMO 2024 Problem 1
- This topic has 1 reply, 2 voices, and was last updated 1 year, 5 months ago by
 Cheenta Aryabhatta.
Cheenta Aryabhatta.
- AuthorPosts
- January 21, 2024 at 11:35 pm #98352
 Dr. Ashani DasguptaKeymaster
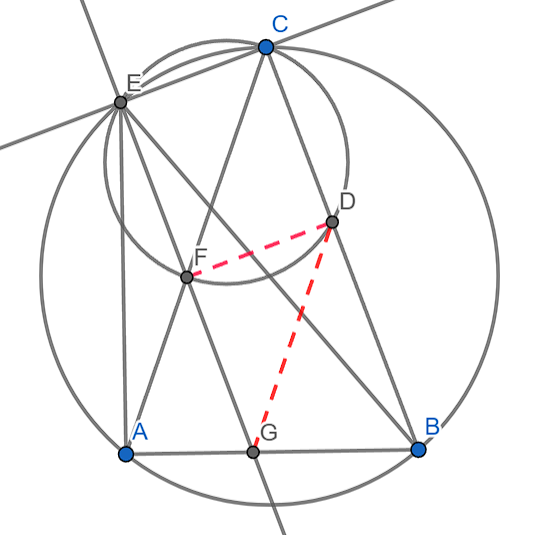
Dr. Ashani DasguptaKeymasterIn triangle \(A B C\) with $C A=C B$, point $E$ lies on the circumcircle of $A B C$ such that $\angle E C B=90^{\circ}$. The line through $E$ parallel to $C B$ intersects $C A$ in $E$ and $A B$ in $C$. Prove that the centre of the circumcircle of triangle $E G B$ lies on the circumcircle of triangle $E C F$.
January 22, 2024 at 6:53 pm #98417 Cheenta AryabhattaParticipant
Cheenta AryabhattaParticipant
Denote the circumcircle of \(\triangle ABC\) and \(\triangle EFC\) as \(\Omega\) and \(\Omega_{1}\) respectively.
Now, notice that \(AF=EF\). We can prove it by simple angle chasing. \(\angle CAB=\angle CBA\) (as \(CA=CB\)) and \(EABC\) is cyclic quadrilateral in \(\Omega\), hence \(\angle FAE=180^{\circ}-\angle CAB-\angle ECB=180^{\circ}-\angle ABC-\angle CEG=\angle AEF\implies AF=EF\) in \(\triangle EFA\).
Suppose, \(BC \cap \Omega_{1}=D\). Join \(DF\) and \(DG\).
\(ECDF\) is a cyclic quadrilateral in \(\Omega_{1}\) and \(\angle ECD=\angle CEF= 90^{\circ}\), hence \(ECDF\) is a rectangle. So, \(EF=CD\). Also, \(AF=FG\) (\(EG||BC \implies \angle FGA=\angle CBA=\angle FAG\)). Hence, \(FG=CD\), but also \(FG||CD\), so \(FCDG\) is a parallelogram.
Now, \(FC||DG\implies \angle DGB=\angle CAG=\angle DBG\), so, \(\triangle DGB\) will also be an isosceles triangle with \(DG=DB\), so the perpendicular bisector of side \(GB\) will pass through \(D\). Again, \(EF=FG\) and \(FD \perp EG \implies FD\) is the perpendicular bisector of side \(EG\). Hence, we have shown that \(D\) is the circumcenter of \(\triangle EGB\). And, we're done.
- AuthorPosts
- You must be logged in to reply to this topic.