- This topic has 1 reply, 1 voice, and was last updated 1 year, 4 months ago by
.
Question
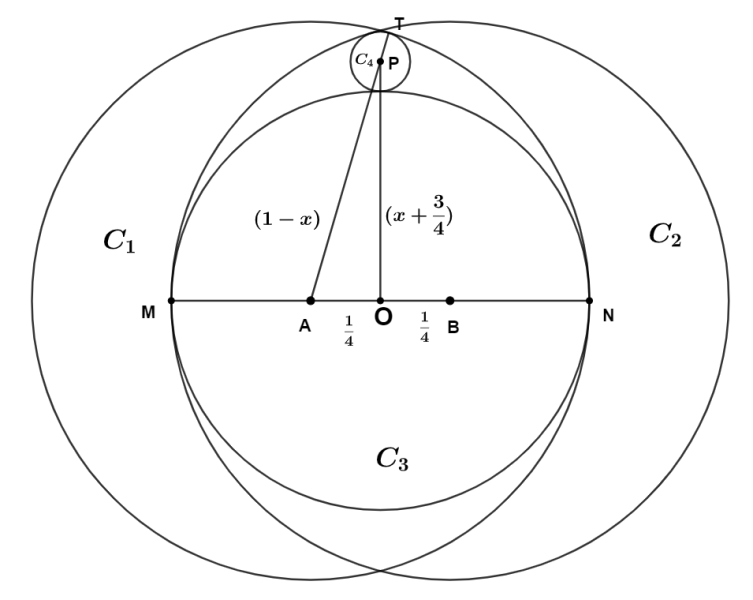
Circle \(C_1\) and \(C_2\) each have radius \(1\) , and the distance between their centers is \(\frac{1}{2}\) . Circle \(C_3\) is the largest circle internally tangent to both \(C_1\) and \(C_2\) . Circle \(C_4\) is internally tangent to both \(C_1\) and \(C_2\) and externally tangent to \(C_3\) . What is the radius of \(C_4\)?
Solution
Taking \(A\) and \(B\) the centres of \(C_1\) and \(C_2\) respectively and the \(C_3\) touches the \(C_1\) and \(C_2\) at \(M\) and \(N\) respectively.
Now, taking mid-point of MN as O.
\(\overline{MO}=\frac{1}{2}\) [As the radius of \(C_2=1\)]
\(\Rightarrow \overline{MA}+\overline{AO}=\frac{1}{2}\)
\(\Rightarrow \overline{MA} +\frac{1}{4}=\frac{1}{2}\)
\(\Rightarrow \overline{MA}=\frac{1}{4}\)
\(\therefore \overline{OM}=\overline{MA}+\overline{AO}=\frac{1}{4}+\frac{1}{2}=\frac{3}{4}\)
\(\therefore\) The radius of \(C_3\) is \(\frac{3}{4}\)
A straight line passing through X and Y, the point of intersection of \(C_1\) and \(C_2\). That line will pass through the point P ,the centre of \(C_4\), and O.
Let’s take the radius of \(C_4\) be \(x\)
Also, \(C_4\) touches the \(C_1\) at a point, say T, so the \(\overline{AT}=1\)
\(\therefore \overline{AP}=1-\overline{PT}=1-x\)
We can now apply Pythagoras Theorem in POM
\(AO^2+OP^2=AP^2\)
\(\Rightarrow \frac{1}{4}^2+(x+\frac{3}{4})=(1-x)^2\)
\(\Rightarrow \frac{1}{16}+x^2+\frac{3x}{2}+\frac{9}{16}=1-2x-x^2\)
\(\Rightarrow \frac{3x}{2}+2x=1-\frac{10}{16}\)
\(\Rightarrow \frac{7x}{2}=\frac{3}{8}\)
\(\Rightarrow \boxed{x=\frac{3}{28}}\) .
- You must be logged in to reply to this topic.