[Dr. Ashani Dasgupta]

Swatik,

Here are some hints. First look at the diagram:

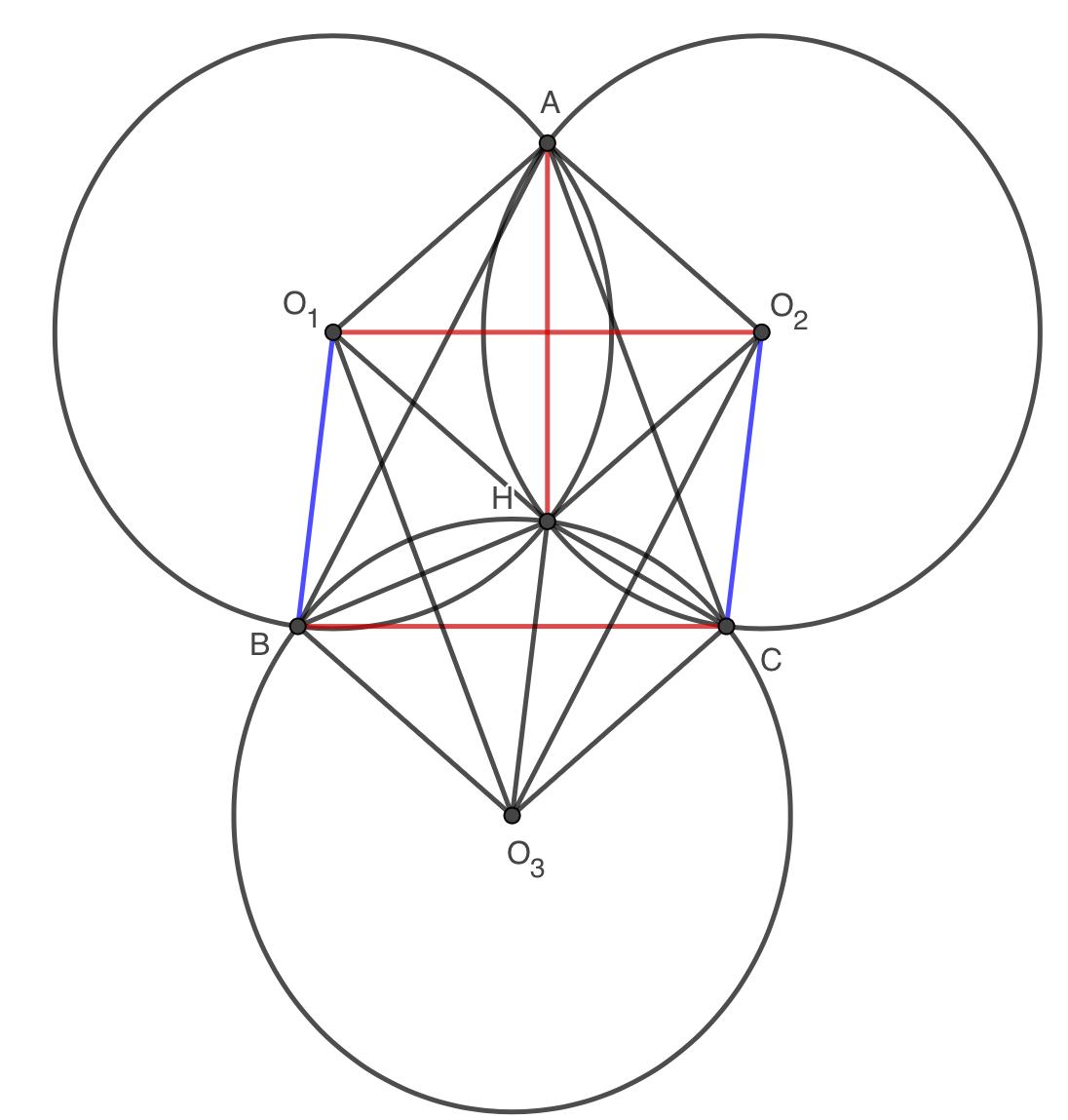
Note that orthocenter is the intersection point of the altitudes of a triangle.

We wish to show \( AH \perp BC \) (and similarly \(BH \perp AC \) etc. ).

Now can you show AH is perpendicular to a segment parallel to BC? It is clearly marked in the picture but you should think closely why that segment is parallel to BC?

One way to do it is to show that segment and BC are part of a parallelogram. (Note that opposite sides of a parallelogram are equal and parallel).

Finally, can you find a circle of which H is a center? That circle is not drawn in the picture above.

Bonus: This is just for fun. In the picture, we have a hexagon that is equilateral but not necessarily equiangular. This is quite different from what happens with triangles (where equilateral means equiangular).

What can you, in general, say about angles of an equilateral polygon? This is not required for solving this problem. But you may think about it.

[Dr. Ashani Dasgupta]

Pinaki,

Welcome to Cheenta. We have received your payment. Our Center Coordinator will call you today after 1 PM and help you to get access to the classes, mock tests and more.

You may:

• Attend online classes (revision sessions)
• Attend contact classes in our Calcutta Center
• Take mock tests
• Take interview sessions.

We will get in touch with you soon.

Regards,

Ashani Dasgupta

[Dr. Ashani Dasgupta]

Suppose ABCD is the quadrilateral. Then

AB + AC + AD = DA + DB + DC

This implies AB + AC = DB + DC ---(i)

Similarly BA + BC + BD = CA + CB + CD

That is BA + BD = CA + CD (ii)

Substracting (ii) from (i) we have AC - BD = DB - CA

Hence AC = BD

Similarly AB = DC.

Hence ABCD is a parallelogram.

Think! How can you extend this argument to show that this parallelogram is indeed a rectangle?

[Dr. Ashani Dasgupta]

The RMO sessions begin shortly.

[Author]

Posts