[অশনি দাশগুপ্ত]

Proof: Suppose O is the center of the circle S. Join OA and OB.

OA = OB = r (radius).

P be any point on AB. It is sufficient to show OP r would imply it is outside the circle).

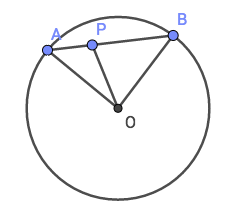
Clearly $latex \angle APO + \angle BPO = 180^0 $ hence

either both are right angles
or one of these angles is obtuse.
WLOG suppose $latex \angle OPB \ge 90^o $. Clearly in $latex \Delta OPB $ it is the largest angle. Hence side opposite to $latex \angle OPB $ is the largest side in $latex \Delta OPB $. Therefore OB > OP.

This implies OP < OB = r hence P is inside the circle.

As P is an arbitrary point on the chord AB, this shows all points on the chord (except A and B) are inside the circle.

[Author]

Posts