[Deepan Dutta]

\(s^3 - 22s^2 + 80s - 67\) should be factorised as \((s-p)(s-q)(s-r)\), as \(p,q\) and \(r\) are the roots of the polynomial \(x^3 - 22x^2 + 80x - 67\).
So, \(1=A(s-q)(s-r)+B(s-r)(s-p)+C(s-p)(s-q)\)

Now for \(s=p\), we would get, \(\frac{1}{A}=(p-q)(p-r)\)
Similarly, for \(s=q\), we get, \(\frac{1}{B}=(q-p)(q-r)\)
And, for \(s=r\), we get, \(\frac{1}{C}=(r-p)(r-q)\)
\(\therefore\) Adding them we can get, \(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}=p^2+q^2+r^2-pq-qr-rp\)
Now form the given equation we can obtain the sum of the roots,
\(p+q+r=22\)
Also the sum of the roots taken two at a time \(pq+pr+rq=80\)
So, \(p^2+q^2+r^2=(p+q+r)^2-2(pq+pr+rq)\)
\(\Rightarrow p^2+q^2+r^2=22^2-160\)
\(\Rightarrow p^2+q^2+r^2=484-160=324\)
So, \(\frac{1}{A}+\frac{1}{B}+\frac{1}{C}=324-80=\boxed{244}\)

• This reply was modified 1 year, 3 months ago by Deepan Dutta.

[Deepan Dutta]

All the edges are \(1\) unit.

Let \(\overline{DF}=x\) unit.

\(\therefore\) \(\overline{C^{\prime}F}=1-x\)

As, \(\angle C^{\prime}DF=90^o\) we can apply the \(\textbf{Pythagorean Theorem}\) on that triangle,

\({\frac{1}{3}}^2+x^2=(1-x)^2\)

\(\Rightarrow x=\frac{4}{9}\)

\(\therefore\) \(FC^{\prime}=\frac{5}{9}\)

Now, if the \(\angle FC^{\prime}D\) be \(\theta\) then \(\angle EC^{\prime}A=90^o-\theta\).

So, \(\triangle AEC^{\prime}\sim\triangle DFC^{\prime}\)

\(\therefore\) \(\frac{DF}{AC^{\prime}}=\frac{C^{\prime}D}{AE}=\frac{C^{\prime}F}{C^{\prime}E}\)

From, \(\frac{DF}{AC^{\prime}}=\frac{\frac{4}{9}}{\frac{2}{3}}=\frac{2}{3}\)

So, \(\frac{C^{\prime}D}{AE}=\frac{2}{3}\Rightarrow AE=\frac{1}{3}\times\frac{3}{2}=\frac{1}{2}\)

\(\frac{C^{\prime}F}{C^{\prime}E}=\frac{2}{3}\Rightarrow C^{\prime}E =\frac{5}{9}\times\frac{3}{2}=\frac{5}{6}\).

So the perimeter of the \(\triangle AEC^{\prime}=\frac{2}{3}+\frac{1}{2}+\frac{5}{6}=\boxed{2}\).

[Deepan Dutta]

If we observe the regular icosahedron carefully then we can understand that it has \(12\) vertices that can be divided into \(4\) layers,

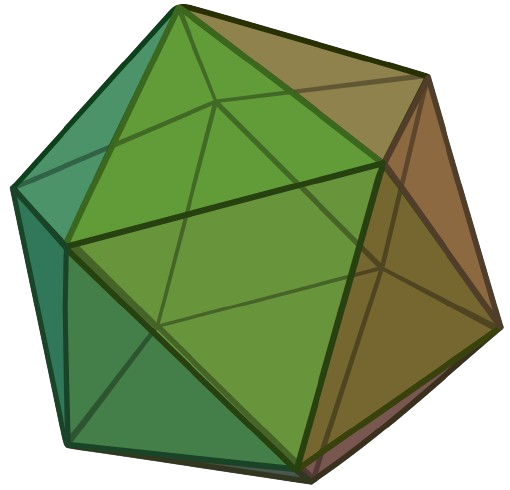
1. Top most point
2. Upper regular pentagon
3. Lower regular pentagon
4. Bottom most point.

So if we try to choose the top most point as \(R\), then there are \({5\choose1}\cdot{6\choose1}\) ways to choose the points \(S\) and \(Q\) respectively,when \(S\) is in the upper regular pentagon layer.

On the other hand If \(S\) is in the lower regular pentagon layer, then \(S\) and \(Q\) can be chosen in \({5\choose1}\cdot{1\choose1}\) ways.

 

\(\therefore\) Probability of choosing three points \(Q,R\) and \(S\) so that \(d(Q, R)>d(R, S)=\frac{{5\choose1}\cdot{6\choose1}+{5\choose1}\cdot{1\choose1}}{{11\choose2}\cdot2!}=\frac{35}{110}=\boxed{\frac{7}{22}}\).

[In \({12\choose1}\) ways we can choose the point \(R\), as that factor is present in both the numerator and denominator so we are not taking that under consideration]

• This reply was modified 1 year, 4 months ago by Deepan Dutta.

[Deepan Dutta]

\(\textbf{Solution}\)

Let the \(\textit{complementary}\) divisors be \((x-10)\) ,\((x+10)\) and \((y-\frac{23}{2})\) and \(y+\frac{23}{2})\).

So, \(N=(x-10)(x+10)=x^2-10^2=x^2-100\)

and, \(N=(y-\frac{23}{2})(y+\frac{23}{2})=y^2-(\frac{23}{2})^2=y^2-\frac{529}{4}\) .

\(\therefore\) \(x^2-100=y^2-\frac{529}{4}\)

\(\Rightarrow y^2-x^2=\frac{529}{4}-100\)

\(\Rightarrow (y+x)(y-x)=\frac{129}{4}\)

\(\Rightarrow 4(y+x)(y-x)=129\)

\(\Rightarrow (2y+2x)(2y-2x)=129\)

\(\Rightarrow (m+n)(m-n)=129\) [Assuming \(2y=m\) and \(2x=n\)]

So, either \((m+n)(m-n)=43\times 3\) or \((m+n)(m-n)=129\times 1\)

• Case I

\((m+n)(m-n)=43\times 3\)

So, \((m+n)=43\) and \((m-n)=3\) because if  \((m+n)=3\) and \((m-n)=43\) then we are having negative solutions of \(x\) and \(y\), which cannot happen.

Now, by adding the equations we have \((m+n)+(m-n)=43+3 \Rightarrow 2m=46\Rightarrow m=23 \Rightarrow 2x=23 \Rightarrow x=11.5\)

\(x\) cannot have a non-integral or a negative solution, so this is not the required solution.

• Case II

Either \(m+n=129\) and \(m-n=1\) or \(m+n=1\) and \(m-n=129\).

But the in the former case we will get the negative solutions of \(n\), so that cannot be a solution.

So, adding the equations we get, \(m+n+m-n=129+1\Rightarrow 2m=130\Rightarrow m=65 \Rightarrow \boxed{y=32.5}\)

Again, \(n=64\Rightarrow \boxed{x=32}\)

\(\therefore\) This is the only possible solution.

So, \(N=(32-10)(32+10)=42\cdot 22 = 924\)

\(\therefore\) The sum of the digits of \(N=\boxed{9+2+4=15}\)

• This reply was modified 1 year, 4 months ago by Deepan Dutta.
• This reply was modified 1 year, 4 months ago by Deepan Dutta.

[Deepan Dutta]

Solution

Taking \(A\) and \(B\) the  centres of \(C_1\) and \(C_2\) respectively and the \(C_3\) touches the \(C_1\) and \(C_2\) at \(M\)  and \(N\) respectively.

Now, taking mid-point of MN as O.

 

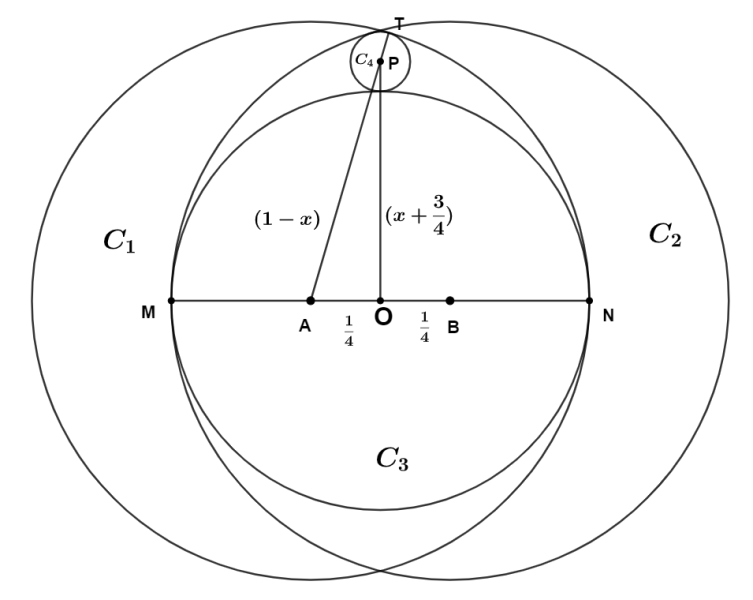
\(\overline{MO}=\frac{1}{2}\) [As the radius of \(C_2=1\)]

\(\Rightarrow \overline{MA}+\overline{AO}=\frac{1}{2}\)

\(\Rightarrow  \overline{MA} +\frac{1}{4}=\frac{1}{2}\)

\(\Rightarrow \overline{MA}=\frac{1}{4}\)

\(\therefore \overline{OM}=\overline{MA}+\overline{AO}=\frac{1}{4}+\frac{1}{2}=\frac{3}{4}\)

\(\therefore\) The radius of \(C_3\) is \(\frac{3}{4}\)

A straight line passing through X and Y, the point of intersection of \(C_1\) and \(C_2\). That line will pass through the point P ,the centre of \(C_4\), and O.

Let’s take the radius of \(C_4\) be \(x\)

Also, \(C_4\) touches the \(C_1\) at a point, say T, so the \(\overline{AT}=1\)

\(\therefore \overline{AP}=1-\overline{PT}=1-x\)

We can now apply Pythagoras Theorem in POM

\(AO^2+OP^2=AP^2\)

\(\Rightarrow \frac{1}{4}^2+(x+\frac{3}{4})=(1-x)^2\)

\(\Rightarrow \frac{1}{16}+x^2+\frac{3x}{2}+\frac{9}{16}=1-2x-x^2\)

\(\Rightarrow \frac{3x}{2}+2x=1-\frac{10}{16}\)

\(\Rightarrow \frac{7x}{2}=\frac{3}{8}\)

\(\Rightarrow \boxed{x=\frac{3}{28}}\) .

• This reply was modified 1 year, 4 months ago by Deepan Dutta.

[Author]

Posts