[Nitin Prasad]

No, just checking for the case where f is decreasing or increasing is not sufficient. As you pointed out, we need to consider the case (if possible) where f is just some random arrangement and doesn't have monotonic property.

Hints

• If  'f'  a one-one function? Observe that if f(m)=f(n) implies m=n then, the given  function is one-one.
• Observe that  $$f[ f(m+k)+f(n-k) ]=m+n=f[ f(m)+f(n) ]$$. What can we conclude?

Using further manipulations you can finally show that f(n)=n. The complete solution has been attached below

[Nitin Prasad]

Consider a polynomial 'f(x)' with 'n' positive real roots given by $$\alpha_1,alpha_2,\cdots,\alpha_n$$. Define-

$$\sigma_k=\frac{S_k}{n\choose k}$$.Now we following two results-

Newton's inequality- $$\sigma_{k-1}\sigma_{k+1}\leq \sigma_k^2$$
Maclaurian inequality- $$(\sigma_{1})^\frac{1}{1}\geq(\sigma_{2})^\frac{1}{2}\geq(\sigma_{3})^\frac{1}{3}\geq\cdots\geq(\sigma_{n})^\frac{1}{n}$$

For proof you may consult following link

https://artofproblemsolving.com/wiki/index.php/Newton%27s_Inequality

Now its clear that the given case is just a special case of maclaurian inequality (n=4)

[Nitin Prasad]

 

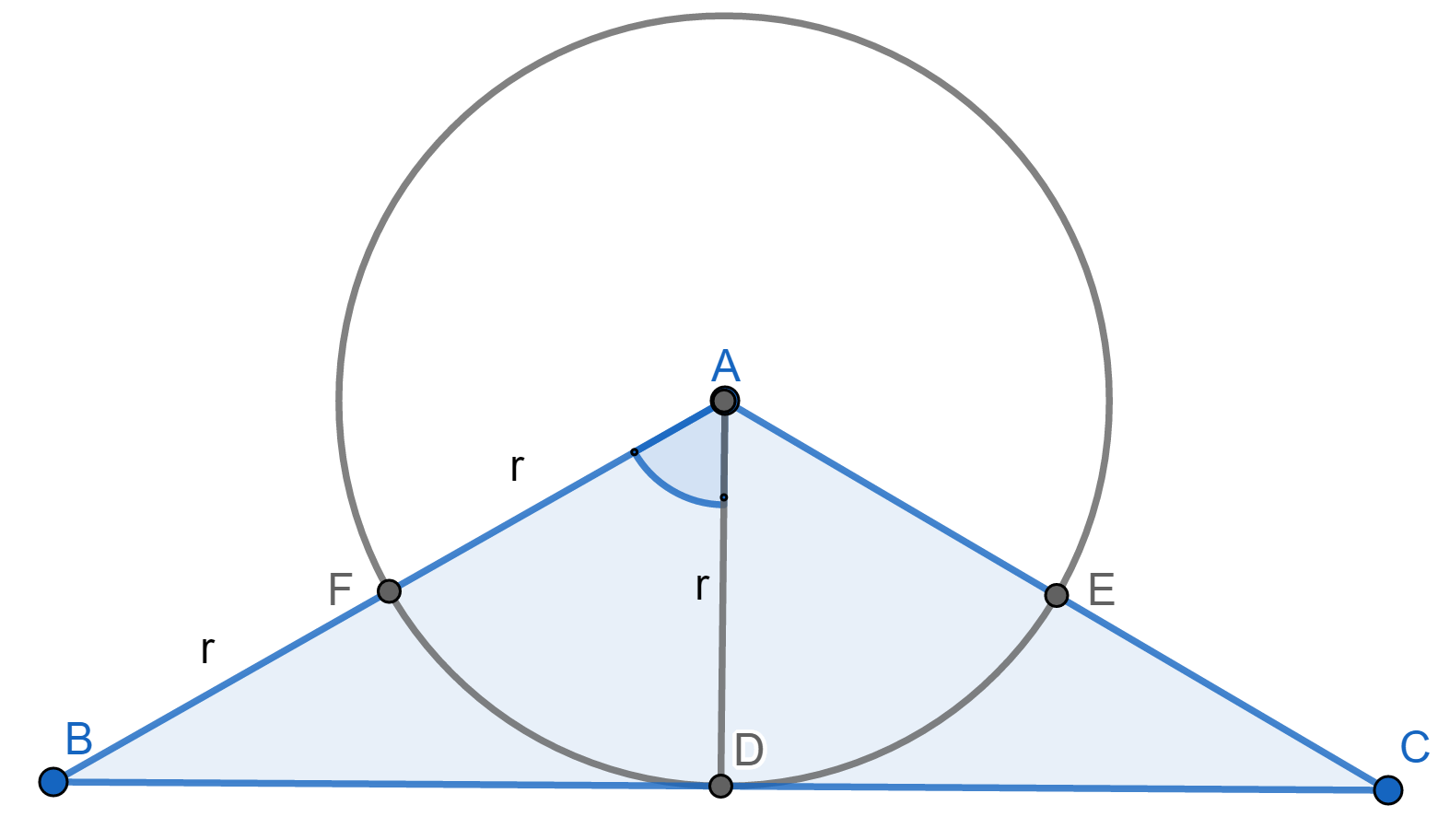
Let D, E, F be midpoints of sides BC, CA, AB respectively. Hence the circle in the above figure is the nine-point circle of triangle ABC

If vertex A is the nine-point center of triangle ABC then following are some of the observations

• AE=AF=r (radius of the circle in the above figure). Therefore AB=AC=2r, hence this condition was redundant.
• AD=r. Since triangle ABC is isosceles, therefore AD is also an altitude, i.e. $$\angle ADC=90^\circ$$
• $$\frac{AD}{AB}=\frac{1}{2}\Longrightarrow \angle BAD=60^\circ$$.

Also observe that whenever in a $$\triangle XYZ, \angle  YXZ=120^\circ \& XY=XZ$$, then X is a nine-point center of triangle XYZ

Hence A is a nine-point center of a triangle ABC if and only if-$$\angle BAC=120^\circ \& AB=AC$$

[Nitin Prasad]

The following figure illustrates the given situation, and we need to show that  $$\frac{AB}{CD}=\frac{OA.OB}{OC.OD}$$

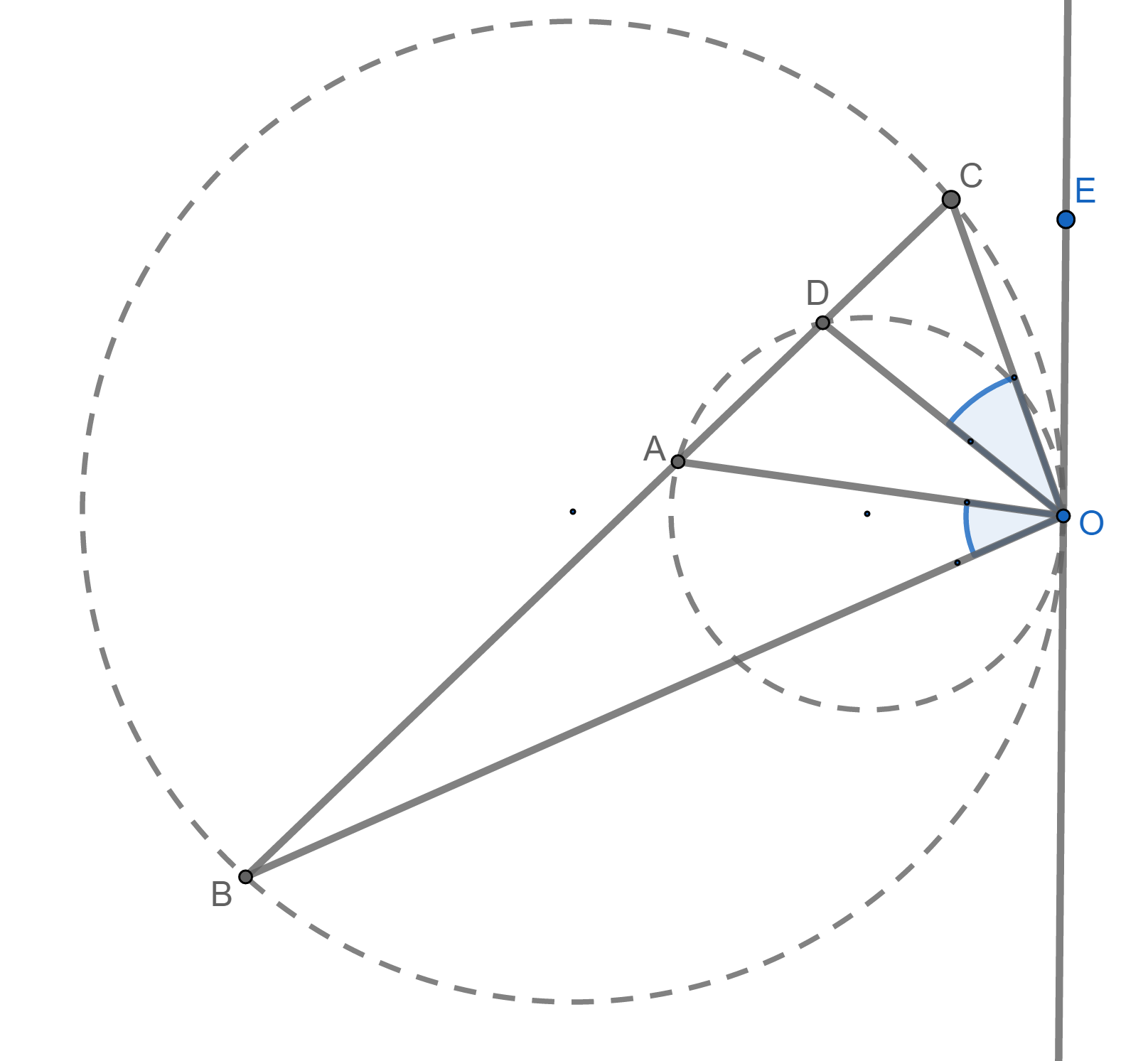
Observe that $$\frac{AB}{CD}=\frac{ar(OAB)}{ar(OCD)}=\frac{\frac{1}{2}OA\cdot OB\sin(\angle AOB)}{\frac{1}{2}OC\cdot OD\sin(\angle COD)}$$

Hence if $$\angle AOB=\angle COD$$ then we are done.
Now observe that $$\angle EOC+\angle COD=\angle EOD=\angle OAD=\angle OBA+\angle AOB=\angle EOC+\angle AOB$$
Hence we have $$\angle AOB=\angle COD$$

Here you should consider directed angles to avoid configuration issues

[Nitin Prasad]

Following is a proof using vectors. Let's denote position vector of point P by $$\vec{P}$$

Let $$\vec{O}=\vec{0}$$,  and then observe that $$\vec{H}=\vec{A}+\vec{B}+\vec{C}$$

Now let signed area of a triangle ABC be (we consider its sign as positive if A,B,C are in antclockwise direction) denoted by (ABC)

 

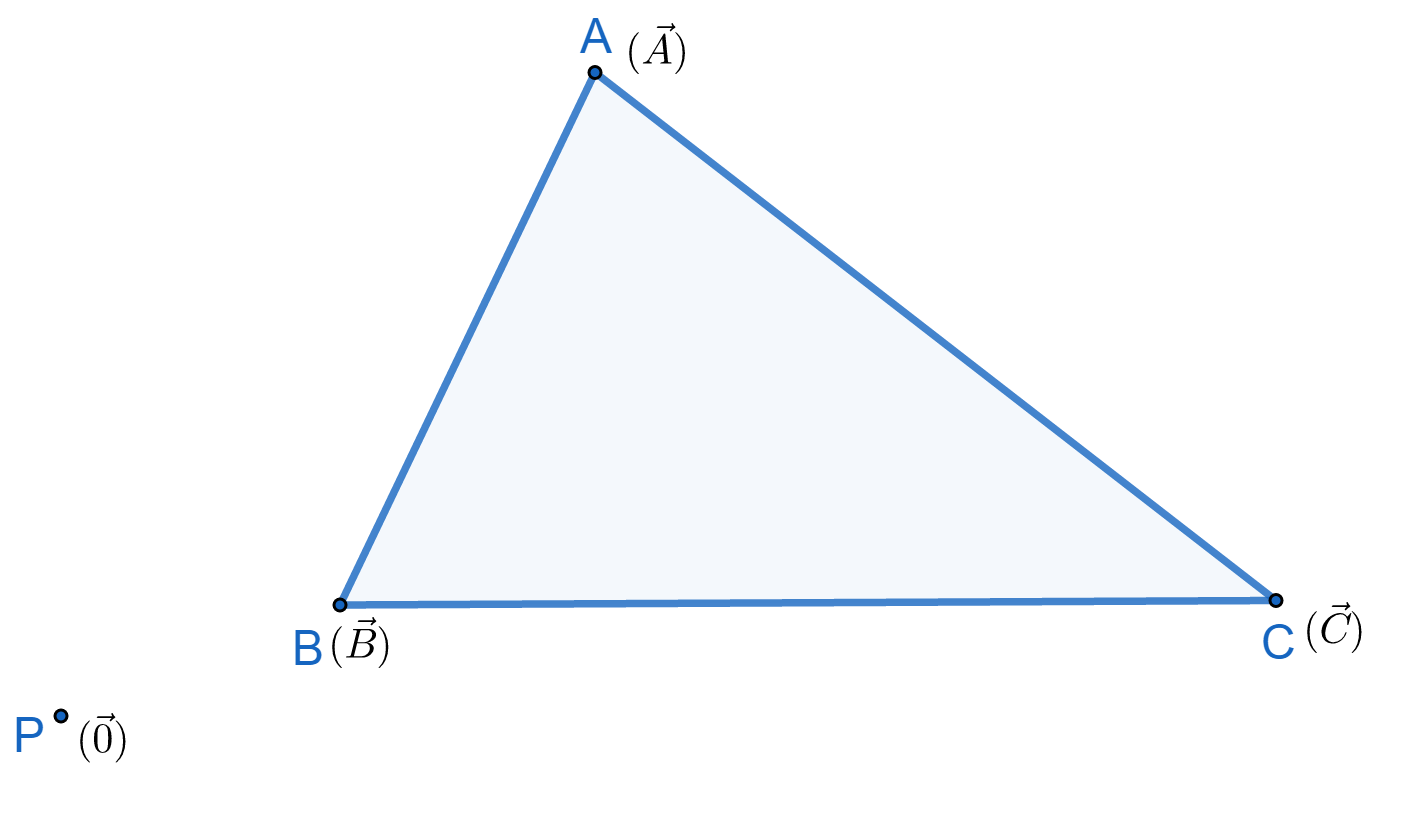
Now observe that $$(ABC)=\frac{1}{2}\vec{BC}\times \vec{BA}=\frac{1}{2}(\vec{B}\times\vec{C}+\vec{C}\times\vec{A}+\vec{A}\times\vec{B})$$

Hence we have

• $$(AOH)=\frac{1}{2}(\vec{A}+\vec{B}+\vec{C})\times\vec{A}$$
• $$(BOH)=\frac{1}{2}(\vec{A}+\vec{B}+\vec{C})\times\vec{B}$$
• $$(COH)=\frac{1}{2}(\vec{A}+\vec{B}+\vec{C})\times\vec{C}$$

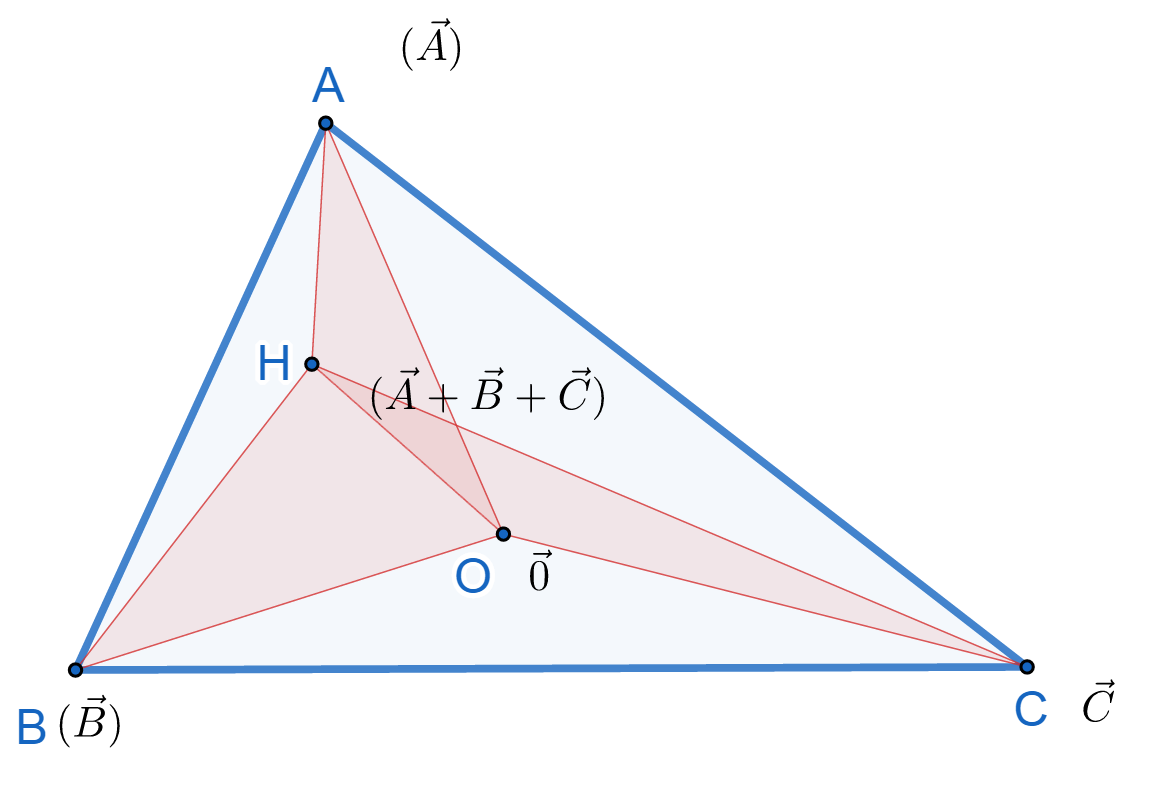
Now if not all three of them are 0, then there are two of the above three signed area have same sign. WLOG let's consider (BOH) and (COH) have same sign, then

$$|AOH|=|-(BOH)-(COH)|=|BOH+COH|=|BOH|+|COH|$$

Hence we have our desired result.

[Author]

Posts