[Cheenta Aryabhatta]

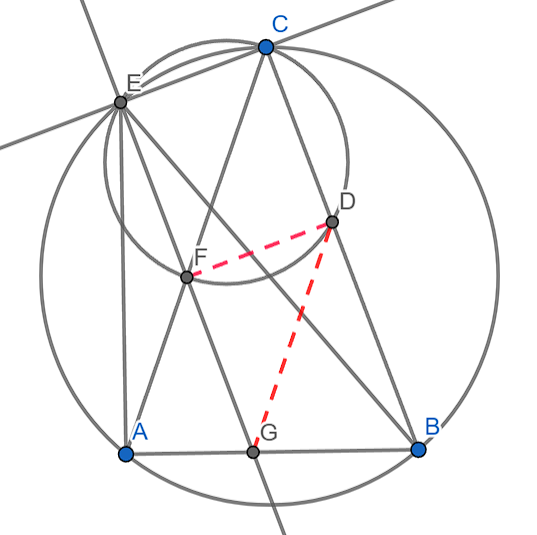
Denote the circumcircle of \(\triangle ABC\) and \(\triangle EFC\) as \(\Omega\) and \(\Omega_{1}\) respectively.

Now, notice that \(AF=EF\). We can prove it by simple angle chasing. \(\angle CAB=\angle CBA\) (as \(CA=CB\)) and \(EABC\) is cyclic quadrilateral in \(\Omega\), hence \(\angle FAE=180^{\circ}-\angle CAB-\angle ECB=180^{\circ}-\angle ABC-\angle CEG=\angle AEF\implies AF=EF\) in \(\triangle EFA\).

Suppose, \(BC \cap \Omega_{1}=D\). Join \(DF\) and \(DG\).

\(ECDF\) is a cyclic quadrilateral in \(\Omega_{1}\) and \(\angle ECD=\angle CEF= 90^{\circ}\), hence \(ECDF\) is a rectangle. So, \(EF=CD\). Also, \(AF=FG\) (\(EG||BC \implies \angle FGA=\angle CBA=\angle FAG\)). Hence, \(FG=CD\), but also \(FG||CD\), so \(FCDG\) is a parallelogram.

Now, \(FC||DG\implies \angle DGB=\angle CAG=\angle DBG\), so, \(\triangle DGB\) will also be an isosceles triangle with \(DG=DB\), so the perpendicular bisector of side \(GB\) will pass through \(D\). Again, \(EF=FG\) and \(FD \perp EG \implies FD\) is the perpendicular bisector of side \(EG\). Hence, we have shown that \(D\) is the circumcenter of \(\triangle EGB\). And, we're done.

[Author]

Posts