Sketching a complex set - I.S.I. Entrance 2019 Subjective Solution Problem 3
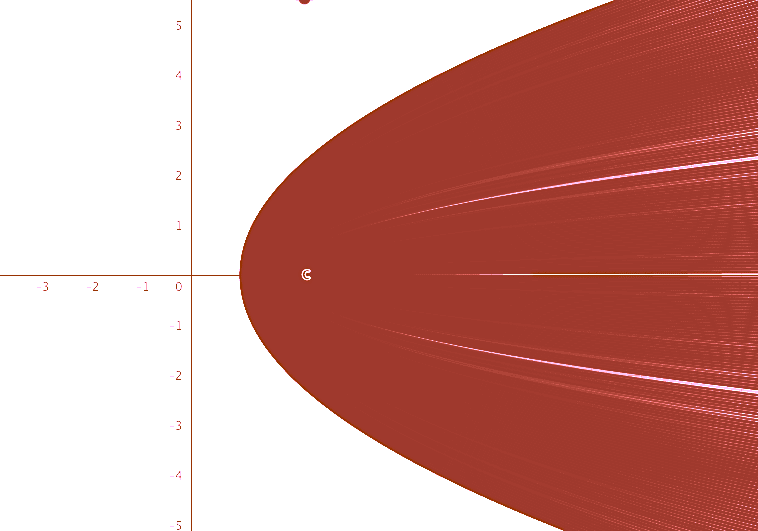
Join Trial or Access Free ResourcesJoin Trial or Access Free ResourcesLet \( \Omega = \{ z = x + i y \ \mathbb{C} : |y| \leq 1 \} \). If \( f(z) = z^2 + 2 \) then draw a sketch of $$ f(\Omega ) = \{ f(z) : z \in \Omega \} $$
Justify your answer.
[/et_pb_text][/et_pb_column][/et_pb_row][et_pb_row _builder_version="3.22.4"][et_pb_column type="4_4" _builder_version="3.22.4"][et_pb_accordion open_toggle_text_color="#0c71c3" _builder_version="3.22.4" body_font="Raleway||||||||" toggle_font="||||||||" text_orientation="center" custom_margin="10px||10px"][et_pb_accordion_item title="Source of the problem" open="on" _builder_version="3.22.4" title_text_shadow_horizontal_length="0em" title_text_shadow_vertical_length="0em" title_text_shadow_blur_strength="0em" body_text_shadow_horizontal_length="0em" body_text_shadow_vertical_length="0em" body_text_shadow_blur_strength="0em"]I.S.I. (Indian Statistical Institute, B.Stat, B.Math) Entrance. Subjective Problem 3 from 2019
[/et_pb_accordion_item][et_pb_accordion_item title="Topic" open="off" _builder_version="3.22.4" title_text_shadow_horizontal_length="0em" title_text_shadow_vertical_length="0em" title_text_shadow_blur_strength="0em" body_text_shadow_horizontal_length="0em" body_text_shadow_vertical_length="0em" body_text_shadow_blur_strength="0em"]Complex Numbers, Level Curves
[/et_pb_accordion_item][et_pb_accordion_item title="Difficulty Level" open="off" _builder_version="3.22.4" title_text_shadow_horizontal_length="0em" title_text_shadow_vertical_length="0em" title_text_shadow_blur_strength="0em" body_text_shadow_horizontal_length="0em" body_text_shadow_vertical_length="0em" body_text_shadow_blur_strength="0em"]5 out 10
[/et_pb_accordion_item][et_pb_accordion_item title="Suggested Book" open="off" _builder_version="3.22.4" title_text_shadow_horizontal_length="0em" title_text_shadow_vertical_length="0em" title_text_shadow_blur_strength="0em" body_text_shadow_horizontal_length="0em" body_text_shadow_vertical_length="0em" body_text_shadow_blur_strength="0em"]Complex Numbers from A to Z by Titu Andreescu
[/et_pb_accordion_item][/et_pb_accordion][et_pb_text _builder_version="3.22.4" text_font="Raleway|300|||||||" text_text_color="#ffffff" header_font="Raleway|300|||||||" header_text_color="#e2e2e2" background_color="#0c71c3" border_radii="on|5px|5px|5px|5px" box_shadow_style="preset3" custom_margin="48px||48px" custom_padding="20px|20px|20px|20px"]Do you really need a hint? Try it first!
[/et_pb_tab][et_pb_tab title="Hint 1" _builder_version="3.22.4"]Understand that the map is from x-y plane to u-v plane. (That is the input of the function is from a two-dimensional place and out put is also in 'another' two-dimensional plane.
The domain includes all points (x, y) such that \( -1 \leq y \leq 1 \). Here is a picture of the domain.
We know that $$ f(z) = z^2 + 2 $$
Start with z = x + iy.
Then \( f(z) = (x + i y)^2 + 2 = x^2 - y^2 + 2 + 2xy i \)
Hence in the output space:
\( u = x^2 - y^2 + 2 \)
\( v = 2xy \)
[/et_pb_tab][et_pb_tab title="Hint 3" _builder_version="3.22.4"]Draw level sets. That is, first find what happens at y = 0.
We know that
\( u = x^2 - y^2 + 2 \)
\( v = 2xy \)
Set y = 0 to get
\( u = x^2 + 2 \)
\( v = 0 \)
Hence this is simply the horizontal ray starting at (2, 0) in the u-v plane.
Finally, find the different level curves by setting y = constant (and then varying this constant between -1 and 1)
Since
\( u = x^2 - y^2 + 2 \)
\( v = 2xy \)
Hence \( \frac {v}{2y} = x \)
Replacing in first equation we have
\( u = \frac{v^2}{4y^2} - y^2 + 2 \)
(Notice y is not 0 as we have handled that case previously).
This is a (family of) parabola(s) in the u-v plane with vertex at \( (2 - y^2, 0) \) and opening to the right.
[/et_pb_tab][/et_pb_tabs][et_pb_text _builder_version="3.22.4" text_font="Raleway|300|||||||" text_text_color="#ffffff" header_font="Raleway|300|||||||" header_text_color="#e2e2e2" background_color="#0c71c3" border_radii="on|5px|5px|5px|5px" box_shadow_style="preset3" custom_margin="48px||48px" custom_padding="20px|20px|20px|20px"]
Indian Statistical Institute and Chennai Mathematical Institute offer challenging bachelor’s program for gifted students. These courses are: B.Stat and B.Math program in I.S.I., B.Sc. Math in C.M.I.
The entrances to these programs are far more challenging than usual engineering entrances. Cheenta offers an intense, problem-driven program for these two entrances.
[/et_pb_blurb][et_pb_button button_url="https://www.cheenta.in/isicmientrance/" button_text="Learn More" button_alignment="center" _builder_version="3.22.4" custom_button="on" button_text_color="#ffffff" button_bg_color="#e02b20" button_border_color="#e02b20" button_border_radius="0px" button_font="Raleway||||||||" button_icon="%%3%%" button_text_shadow_style="preset1" box_shadow_style="preset1" box_shadow_color="#0c71c3" background_layout="dark"][/et_pb_button][et_pb_text _builder_version="3.22.4" text_font="Raleway|300|||||||" text_text_color="#ffffff" header_font="Raleway|300|||||||" header_text_color="#e2e2e2" background_color="#0c71c3" border_radii="on|5px|5px|5px|5px" box_shadow_style="preset3" custom_margin="50px||50px" custom_padding="20px|20px|20px|20px"]
